Teoria dos Conjuntos

Na matemática, estudamos a Teoria dos Conjuntos, área que aborda as coleções de elementos em um conjunto. Trata-se de uma linguagem matemática muito aplicada para a definição de elementos matemáticos. Este tipo de estudo e abordagem começou com os pesquisadores Georg Cantor e Richard Dedekind, no ano de 1870.

Atualmente, a teoria dos conjuntos é um dos primeiros conteúdos importantes ensinados aos alunos pelos professores de matemática, ainda no ensino primário. Os conceitos dessa teoria se dedicam a construir associações e a explicar as operações básicas realizadas com conjuntos, como união ou a interseção de um conjunto, por exemplo.

A teoria dos conjuntos é bastante estudada por matemáticos, em diferentes níveis de complexidade. É uma área muito importante e interessante. Confira algumas informações relevantes sobre essa teoria!

Conceitos básicos

A teoria dos conjuntos é uma teoria matemática. Ela é usada para agrupar elementos, como números, objetos, pessoas, etc. Cada elemento de um conjunto é identificado por uma letra minúscula, que pode ser “a”, “b”, “c”, etc.

Assista à aula do Prof. Gui:

Já os conjuntos propriamente ditos são representados por letras maiúsculas e dentro de chaves { }. Nestes grupos, todos os elementos são separados por vírgulas.

Veja: B = {a,e,i,o,u}

Relações estabelecidas pelos conjuntos

Relação de Pertinência – Indica se um elemento pertence (e) ou não pertence (ɇ) ao conjunto.

Veja: A = {w,x,y,z}. Então temos que: w e A (w pertence ao conjunto A) e j ɇ A (j não pertence ao conjunto A).

Relação de Inclusão – Indica se o conjunto está contido (C), não está contido (Ȼ) ou se ele contém outro conjunto (Ɔ).

Veja:

A = {a,e,i,o,u}

B = {a,e,i,o,u,m,n,o}

C = {p,q,r,s,t}

Dessa forma, temos que:

A C B (A está contido em B)

C Ȼ B (C não está contido em B)

B Ɔ A (B contém A)

Conjunto Vazio – É o conjunto sem elementos. Ele pode ser representado por duas chaves { } e também pelo símbolo Ø.

União, Intersecção, Diferença

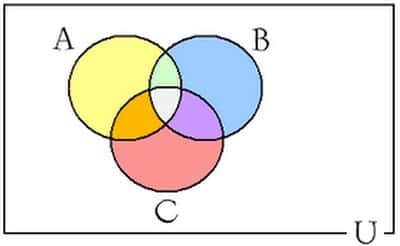
A união dos conjuntos é representada pela letra (U). Ela significa a conexão entre elementos de dois conjuntos diferentes.

Veja:

A = {a,e,i,o,u}

B = {1,2,3,4}

Assim, temos que:

AB = {a,e,i,o,u,1,2,3,4}

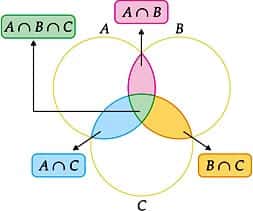
A intersecção dos conjuntos é representada pelo símbolo (∩). Ela significa que existem elementos comuns a dois conjuntos.

Veja:

C = {a, b, c, d, e} ∩ D = {b, c, d}

Então, temos que:

CD = {b, c, d}

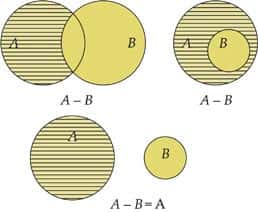
A diferença entre conjuntos é representada por elementos que aparecem em um conjunto, mas que não estão no outro.

Veja:

A = {a, b, c, d, e} – B={b, c, d}

Sendo assim, temos que:

A-B = {a,e}

Igualdade dos Conjuntos

Na relação de igualdade dos conjuntos, temos elementos idênticos em dois conjuntos.

Veja:

A = {1,2,3,4,5}

B = {3,5,4,1,2}

Então, temos que: A é igual a B.