Paralelepípedos
Uma caixa de fósforos, uma embalagem de detergente, um tijolo, algumas caixas de medicamentos, um livro, uma pedra de dominó são objetos com os quais lidamos diariamente e cuja forma se associa a um sólido geométrico a que chamamos paralelepípedo retângulo, pois as faces são perpendiculares às bases e estas são retângulos.
Este sólido geométrico tem os seguintes elementos:
* 6 faces (são retângulos iguais dois a dois);
* 12 arestas (iguais quatro a quatro);
* 8 vértices.
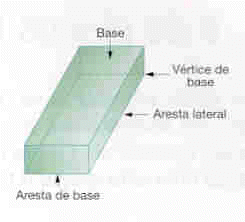
Para a construção de um paralelepípedo é necessário conhecer os comprimentos das três arestas concorrentes a um mesmo vértice.
Através de uma embalagem de cartão de detergente em pó para a roupa, os alunos podem descobrir a relação existente entre a área da sua superfície e a soma das áreas das várias faces. Para isso, os alunos podem abrir a embalagem de detergente com uma tesoura até tornarem a embalagem plana e depois desenharem uma figura que represente a planificação obtida. Nesta altura, os alunos verificarão que a área da superfície de um paralelepípedo retângulo é a soma das áreas das suas faces.
A área do paralelepípedo retângulo é então dada por
A = 2 (ab + ac + bc).
Mas a área deste poliedro pode ser obtida de outra forma. Designando a face em que o paralelepípedo se apoia por base, bem como a face que lhe é oposta, e considerando Ab a área de cada base, p o perímetro de cada base e c a altura, obteremos a área do paralelepípedo retângulo através da seguinte expressão:
A = p.c + 2Ab .
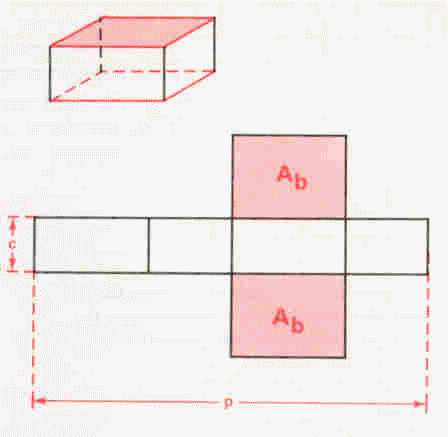
Para determinar o volume deste sólido, consideremos novamente Ab a área da base e c a altura. As seguintes expressões permitem calcular o volume do paralelepípedo retângulo:
* V = Ab . c
* V = a . b . c (pois Ab = a . b).
Porém, nem todos os paralelepípedos são retângulos. No caso das bases do paralelepípedo serem quadrados e não retângulos, o paralelepípedo chama-se paralelepípedo recto. Mas também existem paralelepípedos oblíquos, que são poliedros cujas faces são seis paralelogramos iguais dois a dois. Através do Princípio de Cavalieri, justifica-se que o volume do paralelepípedo oblíquo é também obtido pelo produto da área da base pela altura.
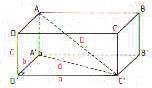
Sejam a, b e c os comprimentos das arestas concorrentes a um mesmo vértice, e que representam os três comprimentos possíveis das doze arestas. A diagonal D é a hipotenusa do triângulo [AA’C’] , retângulo em A’: D2 = d2 + c2. Mas d é a hipotenusa do triângulo [A’D’C’] , retângulo em D’, logo d2 = a2 + b2, e portanto, D2 = a2 + b2 + c2, ou seja, D = 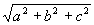 .
.
Planificação:
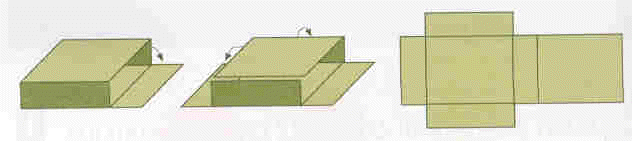
Fonte:
http://www.educ.fc.ul.pt/icm/icm99/icm21/paralelepipedo.htm







