Estudo Analítico do Ponto

O estudo analítico do ponto tem como base o plano cartesiano que orienta a localização dos pontos no espaço. Entenda mais sobre esse estudo!

Na matemática, temos o estudo da Geometria Analítica, que contempla a análise das propriedades das figuras geométricas. Dentro dessa área, uma das matérias abordadas é o estudo analítico do ponto.

Esse tipo de estudo está relacionado ao Plano Cartesiano, criado por René Descartes, e que ajuda a localizar os pontos no espaço. As características do ponto são as primeiras instruções passadas aos alunos no estudo da Geometria Analítica.

Todo ponto possui coordenadas de localização. Assim, é possível encontrar o ponto médio de um segmento e até a distância entre dois pontos no mesmo espaço.

Veja exemplos de estudos analíticos dos pontos:

A primeira característica do ponto é que os pontos são considerados alinhados quando são colineares, ou pertencem a uma mesma reta.

Em seguida, temos que, partindo do princípio de que temos dois eixos – Eixo Y (linha vertical) ou eixo das ordenadas, e Eixo X (linha horizontal) ou eixo das abscissas – podemos encontrar a localização de um ponto P entre as duas coordenadas X e Y. Nesse cenário, podemos determinar em que lugar dos eixos das ordenadas e abscissas o ponto se encontra. Essa situação é representada por (Xp, Yp)

Outro conceito importante é o de bissetrizes, que são retas que cortam exatamente o centro do plano cartesiano, formando um ângulo de 45º com os eixos X e Y. As coordenadas dos pontos da bissetriz que estão nos quadrantes pares são sempre opostos. Os pontos sobre a bissetriz dos quadrantes ímpares, têm valores iguais para X e Y.

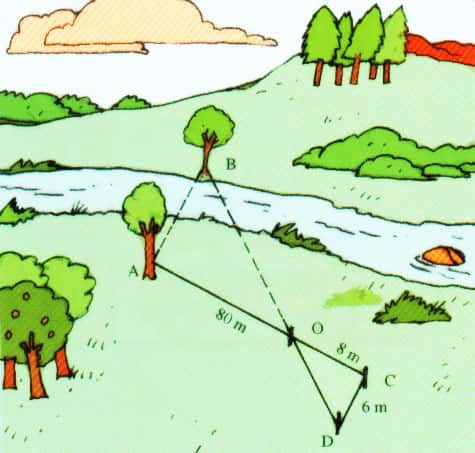
Também é possível determinar a distância entre dois pontos. Para isso, é preciso saber as coordenadas de dois pontos no plano cartesiano (ponto A e B). Essa distância é calculada com base no teorema de Pitágoras – a² = b² + c².

Outras características do ponto que podem ser determinadas na Geometria Analítica são: o ponto médio de um segmento, o baricentro de um triângulo e a condição de alinhamento dos pontos.