Eratóstenes calcula a circunferência da Terra
Eratóstenes, conhecido por calcular a circunferência da Terra, era natural da Grécia, vivendo no período que corresponde ao século 3 a.C. Como vivia no Egito, na Alexandria, onde trabalhava na Biblioteca de Alexandria, tinha muito contato com o conhecimento que estava acumulado nos livros e papiros.
E foi justamente em uma publicação que ele teria achado informações de que em Assuã, uma região localizada a 800 km de Alexandria, sempre em 21 de junho, quando o sol marcava meio-dia, o sol não gerava sombra em uma vareta que estava fincada no chão.
Eratóstenes era reconhecido por sua postura de curioso e interessado e teve uma grande sacada: viu que, em Alexandria, quando o sol estava na mesma posição de meio-dia, a sombra não era igual. Este fenômeno mostrara ao rapaz observador que, caso o mundo fosse plano, a sombra seria idêntica, no mesmo horário, em qualquer localidade do planeta!

Eratóstenes
O primeiro raciocínio foi óbvio: de que o planeta deveria ser curvo e que o tamanho da curva da superfície do planeta impactaria diretamente no tamanho da sombra. Por isso, pela distância do sol, a chegada da luz ao planeta ocorreria com raios na posição paralela.
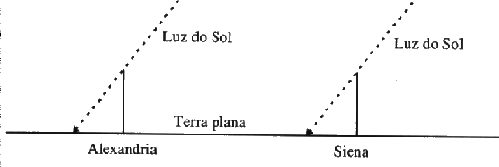
Logo, ele pensou em uma experiência: várias varetas deveriam ser fincadas no chão, em localidades distintas, para comprovar que as sombras seriam diferentes, cada uma com um comprimento, utilizando o sol do mesmo horário.
Para isso, Eratóstenes calculou o comprimento da sombra no dia 21 de junho na cidade de Alexandria, justamente na data em que, em Assuã, a vareta ficava totalmente sem sombra. Para mostrar que estava certo, em Alexandria, a sombra medida ficou em um ângulo de 7°.
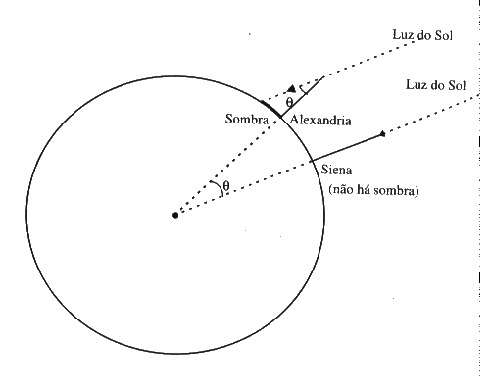
Outra conclusão importante para a época: caso as varetas fossem extremamente compridas, elas poderiam se esbarrar no centro terrestre. Depois do primeiro experimento, Eratóstenes elaborou uma teoria geométrica muito simplificada. Os ângulos de duas retas quando se encontram com outra transversal são idênticos.
Neste caso, o raio do sol é simbolizado pelas retas paralelas, enquanto a reta transversal representa a vareta e o centro do planeta. Ambos os ângulos possuem o mesmo valor, de 7°, representando uma pequena fração do tamanho da circunferência do planeta e, nesse caso, equivalendo à distância entre Alexandria e Assuã!
7° de circunferência da Terra = 800 km!
Como foi comprovado por Eratóstenes, ele obteve a seguinte fórmula:
- Se 7° é igual a 800 km
- Então 360° (uma circunferência completa) é igual a quantos km?
- Resposta = 40 mil km!
Na Linha do Equador, atualmente, a Terra é medida em 40.072 km. Ou seja, a diferença no cálculo de Eratóstenes foi de apenas 72 km, um valor pífio se considerada a escassa tecnologia da época, no século 3 antes de Cristo!

O método utilizado por ele para elaborar o raciocínio geométrico atualmente é sabido que é muito simples, fazendo parte da matéria do Ensino Fundamental.
Veja também:







